Algorytmika, czyli reguły zabawy

W bieżącym rozdziale będziemy rozpatrywać sposoby, jakich używa się w praktyce przy opisie schematów postępowania. Zaczniemy od opisów nieformalnych, a skończymy na takich, które mogą być podstawą automatyzacji.

Postawienie zadania

Za każdym razem, kiedy jest mowa o przetwarzaniu danych, chodzi o wykorzystanie pewnej istniejącej informacji w celu wygenerowania na jej podstawie informacji w jakimś sensie użytecznej. Przedmiotem zainteresowania uczynimy nie tyle same wyniki, co sposoby ich otrzymywania, a ściślej — takie sposoby ich otrzymywania, które da się opisać. Myślimy przy tym o opisach na tyle kompletnych i na tyle precyzyjnych, by dało się je traktować jako instrukcje do wielokrotnego, pomyślnego i bezmyślnego wykonywania.

Niezależnie od celu, w jakim ma zostać podjęte przetwarzanie informacji, i od planowanego sposobu tego przetwarzania, na wstępie niezbędne jest określenie

1. zestawu wymaganych danych wejściowych,
2. zestawu oczekiwanych wyników,
3. warunków spełnianych przez dostarczane dane wejściowe.

Określenie takie będziemy nazywać specyfikacją użytkową zagadnienia przetwarzania. Charakteryzuje ona działanie pożądanego schematu przetwarzania obserwowane z zewnątrz, bez zagłębiania się w szczegóły przekształcania danych.

Z punktu widzenia osoby zainteresowanej otrzymaniem wyników (nazwijmy ją użytkownikiem) postawienie specyfikacji jest najważniejszym etapem przygotowania „frontu działania”. Jeżeli tylko zadanie jest rozwiązywalne, to zawsze istnieje bardzo wiele (tak naprawdę jest ich nieskończenie wiele) sposobów, w jaki dane wynikowe można by otrzymać z danych wejściowych. Żaden z tych sposobów nie interesuje użytkownika sam z siebie, prawdę mówiąc jest mu wszystko jedno, który z nich zostanie zastosowany — dany sposób postępowania można w każdej chwili zastąpić innym sposobem, byle miał on tę samą specyfikację danych.

Dane wejściowe

Jakie dane?

Co oznaczają?

W jakiej postaci dostarczone?

Jakie warunki muszą spełniać?

Oczekiwane wyniki

Jakie dane?

Co oznaczają?

W jakiej postaci?

Warunki dodatkowe

Czy dostawca danych gwarantuje ich bezbłędność?

Co zrobić, kiedy dostarczone dane nie są zgodne ze specyfikacją?

Co zrobić, kiedy nie ma rozwiązania?

Co zrobić, kiedy jest wiele rozwiązań?

Kilka przykładów specyfikacji użytkowych

Wyznaczanie rozwiązań równania algebraicznego

Rozważmy dla przykładu możliwe sposoby wyznaczania pierwiastków równania algebraicznego ax² + bx + c = 0. Poszczególne realizacje tego zagadnienia mogą pobierać dane w kolejności a, b, c lub innej; mogą wyznaczać pierwiastki różnymi sposobami (np. za pomocą wyróżnika, z wzorów Viète’a lub metodami przybliżonymi); mogą wyznaczać rozwiązania rzeczywiste lub zespolone; mogą zwracać sensowne wyniki zawsze albo tylko wtedy, kiedy równanie jest równaniem kwadratowym (tzn. kiedy a ≠ 0); mogą wreszcie udostępniać wyniki w różnej kolejności, w różnej postaci i z różną dokładnością.

Poniżej zamieszczono kilka różniących się między sobą przykładów takich opisów.

Sumowanie danych liczbowych

Rozpatrzmy inne sensowne zagadnienie, jakim jest sumowanie ciągu danych liczbowych. Oto kilka jego możliwych specyfikacji użytkowych:

W przypadku drugim pusty ciąg wejściowy jest niedopuszczalny.

Jeżeli rozpatrzymy następujący zbiór danych wejściowych:

2	0
2.5	3
4	5

to w myśl pierwszej specyfikacji wszystkie sześć liczb zostanie do siebie dodanych i otrzymamy wynik

6	16.5

Według drugiej specyfikacji pierwsza dana oznacza liczbę składników, wynikiem będzie więc

2.5

gdyż taka jest suma liczb: drugiej i trzeciej.

Specyfikacja trzecia każe pomijać wszystko poza pierwszymi liczbami w każdym wierszu, co prowadzi do wyniku

3	8.5

Algorytmy

Zadaniem specyfikacji danych jest stwierdzenie, co powinno być zrobione. Niestety, a może na szczęście, rzeczy nie robią się same. Dlatego ktoś gdzieś musi podjąć wysiłek opisania, w jaki sposób osiągnąć zamierzony cel. Opis ten ma zatem charakter pewnego typu instrukcji postępowania, która powinna być możliwie precyzyjna, a zarazem możliwie ogólna.

Jak od danych wejściowych dojść do wyników?

Postawimy się teraz w roli konstruktorów i krytyków schematu przetwarzania. W odróżnieniu od użytkownika, dla którego najciekawsza jest możliwość otrzymania wyników i same wyniki, nas będzie interesować, w jaki sposób z dostarczonych danych mają powstawać dane wynikowe, i dlaczego taki czy inny sposób tworzenia tych wyników jest — lub nie jest — odpowiedni. Celem naszym będzie budowanie takich schematów. Będziemy się też starać wykazać, że w istocie dla każdego możliwego, lecz sensownego zestawu danych wejściowych, generowane przez konkretny schemat dane wynikowe są (lub nie są) zgodne z oczekiwaniami użytkownika wyrażonymi w specyfikacji.

Żeby te cele zrealizować, analizowany schemat musimy skonfrontować z narzuconą specyfikacją danych; bez niej wszystko sprowadzi się do doraźnych manipulacji na danych. Oczywiście nic nie stoi na przeszkodzie, byśmy specyfikację tę określili sami; więcej: może ona powstawać równolegle z samym schematem — jednak schemat postępowania uznany przez nas za ostatecznie obowiązujący musi być logiczną konsekwencją przyjętej ostatecznie specyfikacji.

Do czego potrzebne są dane?

Z dotychczasowych rozważań popartych przykładami wyprowadzimy dość istotny wniosek. Specyfikacja danych określa, w jakiej postaci dane mają być dostarczone, precyzuje ich sens, ale nie precyzuje ich zawartości. Istnieje przepaść między stwierdzeniem oblicz sumę liczb, które zostaną podane, przy czym pierwsza liczba mówi o ilości składników, a oblicz sumę trzech liczb: 2, 3.5 i −0.2. Tylko to pierwsze jest specyfikacją. Drugie jest konkretnym zestawem danych lub co najwyżej przykładem obrazującym specyfikację.

Schematy przetwarzania należą do tej sfery informacji, która — w odróżnieniu od danych — opisuje sterowanie. Schematy takie można i warto rozpatrywać, a także zapisywać i przechowywać, niezależnie od danych. Sam schemat pozostaje niezmienny przy kolejnych przypadkach jego użycia, mimo że otrzymywane za jego pomocą wyniki mogą być inne dla każdego zestawu danych. Co więcej, przy każdej z rozpatrywanych wyżej specyfikacji użytkowych istnieje potencjalnie nieskończenie wiele zgodnych z nią zestawów danych wejściowych; każdy z nich będzie w pełni obsłużony przez ten sam, zamknięty w skończonej formie schemat postępowania, zwany algorytmem.

Zatem: do opracowania ciągu instrukcji specyfikacja jest potrzebna, ale zestaw danych nie. Do przeprowadzenia obliczeń potrzebny jest gotowy ciąg instrukcji oraz zestaw danych; ze specyfikacji korzysta się tylko pośrednio.

Właściwości algorytmów

Algorytmem nazwiemy ścisły przepis postępowania, którego przestrzeganie gwarantuje otrzymanie danych wynikowych z dostarczonych danych wejściowych w skończonym czasie zgodnie ze specyfikacją użytkową danego problemu. Szczegóły sformułowania algorytmu nie są przy tym związane bezpośrednio ze specyfiką wykonawcy. Algorytm stanowi ogólny schemat i może być zapisywany w różnych językach i konwencjach, zależnie od potrzeb, upodobań autora i wymagań wykonawcy. Oto podstawowe właściwości, którymi musi się cechować każdy algorytm:

zgodność ze specyfikacją

Algorytm jest rozwiązaniem problemu przetwarzania danych. Jeżeli nie postawiono problemu, nie ma sensu mówić o rozwiązaniu.

generowanie wyników

Algorytm opisuje sposób otrzymania danych wynikowych. Celem użycia algorytmu jest otrzymanie konkretnego wyniku. Algorytm, który nigdy nie daje żadnych wyników, jest równoważny niepodejmowaniu żadnej czynności.

ogólność ze względu na wykonawcę

Sformułowanie algorytmu nie powinno zakładać, że wykonawca posiada jakieś specyficzne właściwości. W szczególności nie precyzuje się, kim czy też czym on jest w istocie: człowiekiem, grupą ludzi, maszyną czy też zespołem maszyn. Wynika stąd, że opis algorytmiczny nie może odwoływać się do wiedzy, inteligencji, doświadczenia wykonawcy; nie może też korzystać z analogii. Konieczne jest jednak założenie, że wykonawca „sam z siebie” rozumie znaczenie instrukcji zwanych elementarnymi, które mają prawo pojawić się w algorytmie bez ich definiowania czy objaśniania.

jednoznaczność

W algorytmie nie ma miejsca na dowolność interpretacji ani na pozostawienie ostatecznej decyzji wykonawcy; trzeba precyzyjnie określić przebieg każdego etapu działań i ich kolejność.

skończoność

Niezależnie od tego, czy liczba przewidzianych do wykonania czynności jest z góry znana, czy też zależy od danych, zapis poleceń musi być ujęty w skończonej formie.

Wymienione wyżej właściwości algorytmów mają charakter definiujący, tak więc musi posiadać je każdy algorytm. W praktyce cenione są algorytmy, które posiadają szereg dodatkowych, pożądanych właściwości. Oto najważniejsze z nich:

ogólność ze względu na dane

Sformułowanie algorytmu pozwala rozwiązać całą klasę podobnych zadań, różniących się parametrami ustalanymi za pośrednictwem danych wejściowych.

skuteczność

Dla każdego dopuszczalnego zestawu danych wejściowych algorytm powinien wyznaczyć odpowiednie dane wynikowe. Znaczenie pojęcia „dopuszczalny zestaw danych” winno być wyjaśnione w specyfikacji danych; im szerszą klasę danych ono obejmuje, tym lepiej.

właściwość stopu

Dla możliwie szerokiej klasy danych wejściowych algorytm powinien zatrzymać się w skończonym czasie (po wykonaniu lub mimo niewykonania postawionego zadania).

efektywność

Algorytm powinien osiągać efekt końcowy możliwie niskim kosztem. Koszty eksploatacji są związane z czasem pracy wykonawcy: im bardziej efektywny algorytm, tym mniej czasu zajmie jego wykonanie temu samemu wykonawcy. Efektywność algorytmów wyraża się za pomocą pojęcia złożoności obliczeniowej; w najprostszym ujęciu charakteryzuje ona pracochłonność wykonania jako funkcję ilości danych wejściowych. Niestety — często algorytmy bardziej efektywne są trudniejsze w realizacji, tym samym więcej czasu musi im poświęcić projektant i programista.

Przy rozwiązywaniu zadań praktycznych znaczenie ma również koszt opracowania i koszt przyszłej konserwacji algorytmu, mierzony wysiłkiem wkładanym w jego ulepszanie, rozbudowę oraz implementację w coraz to innych środowiskach. Algorytmy bardziej skomplikowane są na ogół trudniejsze w opracowaniu, analizie i konserwacji. Mogą za to być wygodniejsze w użytkowaniu.

Ogólność a czynności elementarne

Założenie o ogólności opisu nakłada pewne trudności interpretacyjne. Na przykład przygotowanie zestawu danych do odczytu przez człowieka może fizycznie wiązać się z otwarciem tabeli w książce, z włożeniem nośnika elektronicznego do napędu, z otwarciem pliku za pomocą przeglądarki. Analogiczna czynność wykonywana przez program będzie się odwoływać (na ogół pośrednio) do funkcji zarządzania plikami udostępnianymi przez system operacyjny. Widać stąd, że jeżeli algorytm ma zachować w pełni ogólny charakter, to trzeba założyć, że wykonawca potrafi sam z siebie wykonywać niektóre czynności — powinny one niejako być „wbudowane” w wykonawcę. Czynności takie będziemy nazywać czynnościami elementarnymi.

Nie istnieje kategoryczny wykaz wymaganych elementarnych umiejętności wykonawcy algorytmów. Zazwyczaj przyjmuje się, że wykonawca potrafi: wykonywać działania arytmetyczne i logiczne, pobierać dostarczane dane, wysyłać dane, zapamiętać pewną ilość wartości w swojej pamięci, znajdować w opisie algorytmu fragmenty o wskazanej etykiecie (np. instrukcji o danym kolejnym numerze) oraz odnajdować i wykonywać dostarczone mu uprzednio ciągi instrukcji lub ich fragmenty. Powinien także być w stanie korzystać z danych otrzymanych drogą wykonania innych dostarczonych mu algorytmów.

Zauważmy, że zarówno ludzie, jak zespoły ludzkie, a także komputery (w sensie maszyn von Neumanna) spełniają te wymagania. Konkretna techniczna realizacja tych umiejętności bywa natomiast najróżniejsza.

Zauważmy też, że zdolność wykonawcy do realizowania zleconych mu działań i korzystania z ich wyników nie ma nic wspólnego z inteligencją ani z procesem uczenia się. Przeciwnie: wykonane będzie tylko to, co jest napisane w instrukcji, i dokładnie w ten sposób, w jaki jest napisane. Jeżeli instrukcja zawiera podpunkt nakazujący skorzystanie z innej dostarczonej uprzednio instrukcji, i z danych otrzymanych przez jej wykonanie, to zostanie to zrobione. Wykonawca idealny nie przejawia inicjatywy, i jeżeli nawet jest inteligentny, to nie czyni z tego faktu użytku.

Następstwo czynności

Algorytmiczne instrukcje postępowania zakładają ustaloną kolejność czynności. Można sobie wyobrażać, że czynności te są przeznaczone do realizacji jedna po drugiej, w sensie następstwa logicznego: czynność następna może korzystać z efektu wykonania czynności poprzedzających. W ciągach instrukcji następstwo logiczne realizuje się za pośrednictwem następstwa czasowego, ustalając kolejność wykonania poszczególnych instrukcji. Zatem na każdym etapie opisu musi być jasne, która konkretnie instrukcja jest przewidziana do wykonania w następnej kolejności.

Nie znaczy to, że instrukcje zawsze są wykonywane jedna po drugiej w kolejności, w jakiej zostały napisane bądź przekazane systemowi. Niektóre instrukcje pozwalają decydować, czy w ogóle w danej sytuacji podejmować podległą im czynność, a inne pozwalają powracać do instrukcji uprzednio już wykonywanych. Takie sterowanie przepływem instrukcji pozwala użyć skończonego, zwartego opisu w stosunku akcji, których trwanie zależy od dostarczonych danych.

Na przykład edytor plików tekstowych ma swój algorytm, którego binarny zapis znajduje się w systemowym pliku wykonywalnym. Algorytm ten, mimo że składa się ze skończonej liczby instrukcji, jest zbudowany tak, by użytkownik mógł korzystać z niego przez czas, jaki uzna za stosowny. W czasie takiej sesji może on przekazać edytorowi za pomocą urządzeń wejściowych (klawiatury, myszki) praktycznie dowolną ilość informacji sterujących, wpływających na zawartość redagowanych plików. Edytor zaś nie powie: dotarłem właśnie do ostatniej instrukcji, więc kończę pracę i nie obsłużę Twoich następnych żądań. Instrukcji jest skończenie wiele, a czas pracy może być dowolnie długi; zatem niektóre instrukcje będą wykonywane wielokrotnie (być może nawet bardzo wiele razy).

Algorytm, jego implementacja i użytkowanie

Niezależnie od tego, jakie zadanie realizuje algorytm, z punktu widzenia użytkownika można go przedstawić w postaci „czarnej skrzynki”, takiej jak na załączonym rysunku.

W celu uzyskania sensownych wyników użytkownik powinien przygotować sensowne dane i zlecić przeprowadzenie przetwarzania według danego algorytmu jakiemuś wykonawcy, np. automatowi. W szczególności sam użytkownik może pełnić rolę wykonawcy (posługując się np. kartką papieru i kalkulatorem).

Algorytm może być użyty tylko pod warunkiem, że odpowiednie dane wejściowe zostaną rzeczywiście dostarczone. W ten sposób pewne ogólne zadanie, którego sposób rozwiązania został podany, zostaje sprowadzone do tego konkretnego zadania, które trzeba rozwiązać właśnie teraz. Dane te muszą być przygotowane w ściśle określony sposób (np. kolejność) i w określonym miejscu (np. w pliku).

W odróżnieniu od specyfikacji użytkowej, która uwzględnia jedynie znaczenie danych oraz warunki, jakie muszą one spełniać, opis użytkowy algorytmu powinien zawierać techniczne szczegóły przygotowania danych.

W dobrze zaprojektowanej implementacji algorytmu użytkownik winien mieć możliwość określenia wartości danych wejściowych bez ingerencji w treść kodu sterującego.

Należy też odróżnić dane wejściowe od stałych uniwersalnych (takich jak np. liczba e, niektóre stałe fizyczne, liczba dni w tygodniu itp.), których wartość nie jest przewidziana do modyfikacji.

W trybie wsadowym dane wejściowe trzeba przygotować przed rozpoczęciem pracy wykonawcy. W trybie interaktywnym dane dostarcza się na żądanie wykonawcy w trakcie jego pracy.

Dane będące efektem działania algorytmu są przekazywane jako tzw. dane wynikowe. Podobnie jak w przypadku danych wejściowych, przy interpretowaniu wyników nie ma miejsca na żadną dowolność.

Sposoby wyrażania algorytmów

W jakiej formie, jakimi środkami zapisywać i przechowywać algorytmy?

Dla kogo w praktyce ma być przeznaczona instrukcja?

• dla człowieka
• dla grupy współpracujących ludzi
• dla człowieka posługującego się systemami komputerowymi
• dla systemu automatycznego (pojedynczej maszyny, grupy maszyn)

Jakich środków i pojęć użyć, by opis był zrozumiały dla wykonawcy należącego do danej grupy?

Jak łatwe (albo jak trudne) będzie odczytanie i realizacja tej instrukcji przez wykonawcę należącego do innej grupy?

Jak łatwe (albo jak trudne) będzie przepisanie tej instrukcji dla innego wykonawcy?

Język naturalny

Instrukcję taką da się przygotować w języku naturalnym, lecz trzeba przyjąć kilka wstępnych założeń. Po pierwsze nie będziemy zakładać, kim czy też czym jest wykonawca; po drugie trzeba przyjąć, jakie czynności podejmowane przez wykonawcę mają być traktowane jako elementarne. Po trzecie, nie będziemy wymagać od wykonawcy, by rozumiał sens podejmowanych czynności; nie możemy więc apelować do jego wiedzy ani doświadczenia.

Przykłady opisów algorytmu w języku naturalnym

Zauważmy, że w ten sposób ludzie mogą sumować „na piechotę” dowolnie długie kolumny liczb (inny sposób, znany jako dodawanie pisemne, jest łatwiejszy dla ludzi, ale wymaga wracania do poszczególnych składników). Ten sam sposób da się zastosować także w sytuacji, kiedy jedna osoba (użytkownik) czyta liczby, a druga (wykonawca) obsługuje kalkulator kieszonkowy z pamięcią.

Zalety i wady notacji w języku naturalnym

1. łatwość sformułowania (+)
2. łatwość rozumienia bez konieczności specjalistycznego wykształcenia (+)
3. niejednoznaczność języka potocznego (−)
4. bariera językowa między ludźmi (−)
5. niemożność automatycznej interpretacji (−)
6. oddzielenie sterowania od danych (dane nie występują w instrukcji) (+)

Język grafiki

Drugim ważnym środkiem opisywania ciągów czynności są schematy graficzne. W niektórych sytuacjach korzystanie z nich jest bardzo wygodne. Istnieje kilka ważnych notacji graficznych odwzorowujących schematy algorytmiczne. Jedna z nich nosi nazwę sieci działań.

Schematy graficzne sieci działań są zbudowane ze standardowych elementów składowych, które można ze sobą łączyć. Reprezentują one następujące składniki budowy algorytmów:

operacje systemowe

(np. rozpoczęcie i zakończenie działania oraz instrukcje użycia innych algorytmów) — oznaczane za pomocą owalu,

instrukcje proste

(tzn. wykonanie pojedynczej operacji niepodzielnej z punktu widzenia wykonawcy) — oznaczane za pomocą prostokąta,

operacje wejścia–wyjścia

(tzn. pobieranie lub wysyłanie danych) — oznaczane za pomocą równoległoboku,

instrukcje decyzyjne

w których wybór dalszej drogi postępowania zależy od spełnienia pewnego warunku logicznego — oznaczane za pomocą rombu z dwoma wyjściami odpowiadającymi możliwym wartościom warunku,

instrukcje wyboru

w których wybór dalszej drogi postępowania zależy od wartości pewnego wyrażenia — oznaczane za pomocą owalu z wieloma wyjściami odpowiadającymi przewidywanym wartościom wyrażenia,

komentarze

(nie mają wpływu na wykonanie, zawierają notatki autora schematu) — oznaczane za pomocą klamry lub nawiasu,

inne instrukcje

które będziemy budować z wyżej wymienionych (np. instrukcje iterowania),

inne instrukcje

których nie będziemy tu potrzebować,

linie skierowane (strzałki)

łączące instrukcje zgodnie z bezpośrednim następstwem wykonywania.

Przykłady

Na poniższym rysunku przedstawiono sieci działań algorytmów rozpatrywanych w tym rozdziale: algorytmu rozwiązywania równania drugiego stopnia (zgodnie ze specyfikacją danych określoną w pierwszym przykładzie dotyczącym tego zagadnienia) oraz algorytmu sumowania danych wejściowych (zgodnie z trzecią spośród podanych specyfikacji tego zagadnienia).

Oprócz sieci działań, specjaliści używają także innych notacji graficznych. Wśród nich ważne miejsce zajmują diagramy stanów oraz UML. Znajdują one zastosowanie nie tylko w opisie algorytmów, ale także w modelowaniu zjawisk i w zarządzaniu.

Zalety i wady notacji graficznej

Przetwarzaniem opisanym za pomocą sieci działań teoretycznie mógłby zająć się człowiek lub maszyna. Człowiek poradzi sobie z interpretacją schematu graficznego posługując się inteligencją, jednak automaty nie są w stanie przetworzyć obrazka przedstawiającego sieć działań na polecenia. Dlatego dla automatów przygotowuje się polecenia w postaci programów zapisanych za pomocą specjalnie do tego celu zaprojektowanych języków.

1. intuicyjność (+)
2. jednoznaczność na poziomie znaczeniowym (+)
3. nieistotność bariery językowej między ludźmi (+)
4. konieczność rozumienia zestawu abstrakcyjnych symboli (±)
5. niejednoznaczność na poziomie prezentacyjnym jeszcze większa niż w przypadku języka naturalnego (co to znaczy taki sam obrazek?) (−)
6. praktyczny brak możliwości przetłumaczenia na tekst i automatycznego wykonania poleceń (−)
7. oddzielenie sterowania od danych (dane nie występują w schemacie) (+)

Języki programowania

Języki programowania są powszechnie przyjętym środkiem służącym do opisu algorytmów. Podobnie jak języki naturalne, języki programowania cechują się regułami składniowymi, na podstawie których pewne konstrukcje językowe są obowiązujące, inne są dopuszczalne, jeszcze inne wreszcie są zabronione. W odróżnieniu od języków naturalnych, reguły składniowe języków programowania wynikają z ich definicji i są jednoznaczne.

Języki programowania są uboższe pod względem składniowym i znaczeniowym od języków naturalnych, lecz górują nad nimi precyzją.

Języki programowania niskiego poziomu są zorientowane na opis toku przetwarzania w kategoriach bezpośrednio dostępnych wykonawcy.

Języki programowania wysokiego poziomu dostarczają narzędzi nakierowanych na opis toku przetwarzania za pomocą pojęć związanych z przedmiotem przetwarzania.

Elementy składni języków programowania

słowa kluczowe

ciągi znaków, których znaczenie dla programu jest określone a priori przez definicję języka

komentarze

tekst, który nie zawiera instrukcji przeznaczonych do wykonywania i w związku z tym powinien być ignorowany przez wykonawcę. Typowe komentarze objaśniają „co autor miał na myśli”; przydają się one przy analizie i rozbudowie kodu źródłowego. Za szczególny rodzaj komentarzy można uważać dokumentację użytkową zintegrowaną z tekstem źródłowym programu

wyrażenia

konstrukcje pozwalające użyć dostępnych wartości, by na ich podstawie obliczać wartość wynikową, którą z kolei będzie można zapamiętać w celu dalszego przekształcania

instrukcje

pojedyncza instrukcja jest rozkazem do wykonania. Język programowania precyzuje sposób zapisu instrukcji i ich znaczenie

następstwo instrukcji

instrukcje są wykonywane w jednoznacznie ustalonej kolejności

podległość instrukcji

instrukcje sterujące przepływem decydują o wykonaniu (lub o niewykonaniu) innych instrukcji, oraz o tym, która instrukcja zostanie wykonana jako następna

Typy notacji programistycznych

Notacja imperatywna

Ten typ notacji koncentruje się na opisie żądanej czynności wg schematu:

Wykonaj czynność D (akcja) na obiekcie P (argument) w sposób określony przez C (opcje).

ls -lR $HOME
dir  /s/b/l %USERPROFILE%
plot2d(sin(x^2), [x, 0, 10]);
scite plik1 plik2 plik3
sortuj(lista)

Notacja imperatywna jest obecna w większości klasycznych języków programowania.

Notacja proceduralna

Notacja proceduralna pozwala budować złożone czynności i nadawać im nazwy. Pozwala to skoncentrować się na logicznym uporządkowaniu opisów czynności i na ich wzajemnych związkach.

W zasadzie każdy współczesny język imperatywny umożliwia notację proceduralną.

Notacja obiektowa

Ten typ notacji koncentruje się na opisie przedmiotu działania wg schematu:

Weź przedmiot P (obiekt) i wykonaj przypisaną mu czynność D (metoda).

Plik/Otwórz za pomocą/SciTE
kartoteka.listuj
mojedane.wykres2d
Drużyna… Padnij!
lista.append(wartość)
lista.sort(wyrażenie)
Blok danych/Sortuj/Wg kolumny Wiek/Rosnąco

Notacja obiektowa umożliwia zwarte formułowanie skomplikowanych czynności oraz związków czynności. Jej atrakcyjność jest też związana z analogiami do sposobu funkcjonowania umysłu.

Notacja deklaratywna

Podejście zwane deklaratywnym znaczy mniej więcej tyle, że zamiast opowiedzieć, jak coś wykonać, mówi się tylko, co ma być zrobione. Wniosek stąd taki, że opis deklaratywny jest bliższy specyfikacji użytkowej, niż opisu algorytmicznego.

Tym niemniej niektóre wyspecjalizowane języki i środowiska wymagają właśnie podania sformalizowanej deklaracji zamierzonego efektu. Za jej przetłumaczenie na tok działania odpowiedzialne są mechanizmy i komponenty systemu ukryte przed użytkownikiem.

Także odpowiednio zaprojektowane języki programowania bardzo wysokiego poziomu pozwalają, by główna część programu miała formę przypominającą notację deklaratywną.

Przykłady

Zalety i wady notacji w językach formalnych

1. jednoznaczność (+)
2. mała nadmiarowość notacji utrudniająca ludziom rozumienie kodu (−)
3. konieczność opanowania sztucznego formalnego języka (−)
4. nieistotność bariery językowej między ludźmi (+)
5. zapis znakowy umożliwiający automatyczną analizę (+)
6. łatwość automatycznej realizacji opisanych działań (+)
7. wpływ wyboru języka na szczegóły realizacyjne (±)
8. oddzielenie sterowania od danych (dane nie powinny występować w kodzie) (+)

Arkusze kalkulacyjne

Ważnym w praktyce środkiem technicznym wspomagającym algorytmiczne przetwarzanie danych są także środowiska robocze arkuszy kalkulacyjnych.

Arkusze kalkulacyjne wymyślono znacznie później, niż języki programowania, bo dopiero w latach 70-tych XX wieku. Środowisko arkusza składa się z ustalonej liczby komórek identyfikowanych przez adres. Każda komórka może przechowywać albo wartość stałą (rozumianą albo jako daną wejściową, albo jako komentarz), albo regułę obliczania swojej wartości na podstawie wartości innych komórek. Reguły takie zwane są formułami.

Środowiska użytkowe arkuszy kalkulacyjnych są jednocześnie i „maszynami” do przekształcania danych, i edytorami. Przejawia się to na kilka sposobów.

Po pierwsze, edytor danych umożliwia interaktywne (ręczne lub półautomatyczne) przekształcanie zbiorów danych pod kontrolą operatora. Do takich operacji należą np.: przemieszczanie komórek, sortowanie, filtrowanie, wybrane techniki grupowania danych.

Po drugie, edytor dokumentów umożliwia traktowanie arkusza obliczeniowego jako sformatowanego raportu z prezentacją wyników obliczeń. Z tym aspektem pracy wiążą się tak istotne elementy, jak formatowanie komórek pod względem typograficznym oraz środki do graficznej prezentacji danych. Właściwości te przyczyniły się do ogromnej popularności arkuszy kalkulacyjnych jako narzędzi pracy.

Jednak pełnią one role pomocnicze w stosunku do funkcji podstawowej, jaką jest przetwarzanie danych za pomocą formuł wpisanych do komórek. Tworzenie i modyfikacja formuł wiąże się z trzecim, najważniejszym aspektem interaktywnej pracy z arkuszem jako edytorem kodu sterującego.

W popularnych podręcznikach i instrukcjach obsługi arkusze kalkulacyjne traktowane są często jako środowiska do doraźnego „obudowywania” raz wpisanych danych formułami, stosownie do zmieniających się zamiarów operatora. Przy takim podejściu komórki arkusza stanowią naturalne miejsce przechowywania danych, nawet jeśli w ogóle nic nie jest na ich podstawie obliczane.

W bieżącym kursie prezentujemy odmienne podejście. Będziemy patrzeć na arkusz kalkulacyjny jak na środowisko realizacji algorytmów. Znaczy to, że wiedząc, co ma być zrobione, i mając uporządkowany obraz tego, jak zamierzony efekt osiągnąć (np. w postaci opisu słownego lub sieci działań), będziemy używać arkusza do opisania i przechowywania możliwie ogólnych instrukcji, których wykonanie zagwarantuje zamierzony efekt. Przy takim podejściu zasadniczym składnikiem, który warto przechowywać w arkuszu, są formuły przetwarzania, zaś dane są niezbędne tylko na etapie użytkowania, a wcześniej testowania, opracowanych zestawów formuł.

Wobec faktu, że obsługa arkuszy kalkulacyjnych jest niemal intuicyjna i prawie nie wymaga znajomości języków programowania, są one bardzo przydatne w praktyce i warto umieć z nich korzystać. Środowisko robocze arkusza kalkulacyjnego jest podstawowym środowiskiem przetwarzania danych dla wielkiej rzeszy użytkowników systemów informatycznych. Jednak powszechny pogląd, że użytkowanie arkusza nie wymaga w ogóle ani programowania, ani kontaktu z językami formalnymi, ani tym bardziej znajomości podstaw algorytmiki, nie znajduje uzasadnienia.

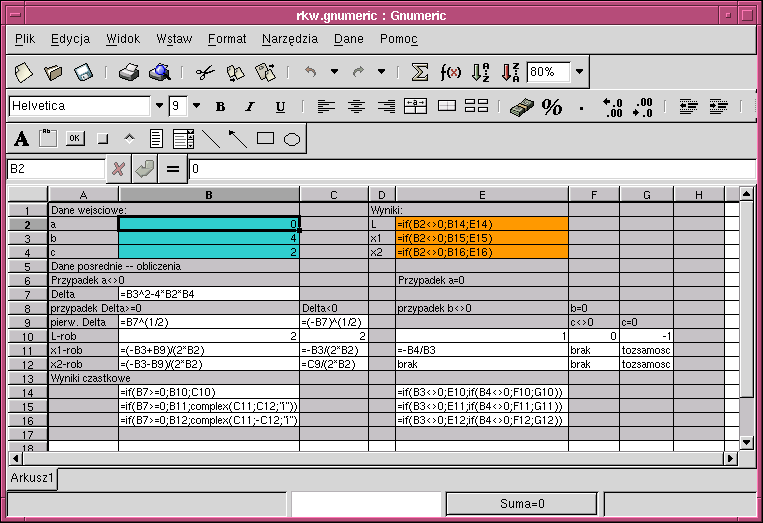
Ilustracja przedstawia przykładowy schemat rozwiązania równania drugiego stopnia za pomocą programu tego typu.

Zalety i wady notacji w postaci arkuszy kalkulacyjnych

1. są łatwiejsze w użyciu od języków programowania (+)
2. wyniki są dostępne „natychmiast” po wprowadzeniu poleceń (+, ale tylko dla prostych przeliczeń)
3. wiele poleceń ma nazwy w języku zbliżonym do naturalnego (ułatwienie dla początkujących) (+)
4. wiele poleceń ma nazwy w języku zbliżonym do naturalnego (bariera językowa) (−)
5. zastąpienie niektórych instrukcji manipulacją (a przynajmniej sprzyjanie takim praktykom) (−)
6. nie każdy algorytm da się łatwo wyrazić za pomocą narzędzi arkusza (−)
7. przemieszanie kodu z danymi (−)
   • konieczność trwałego przechowywania większości danych pośrednich (−)
   • dużo danych → dużo formuł (−)
   • nowy zestaw danych → nowa kopia kodu (−)